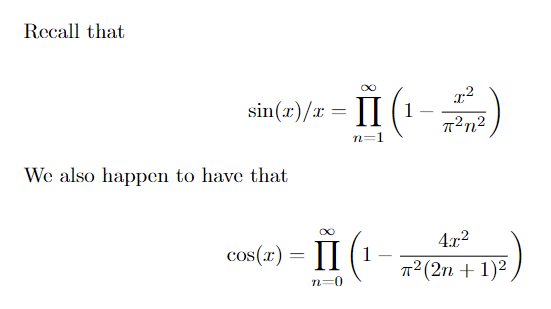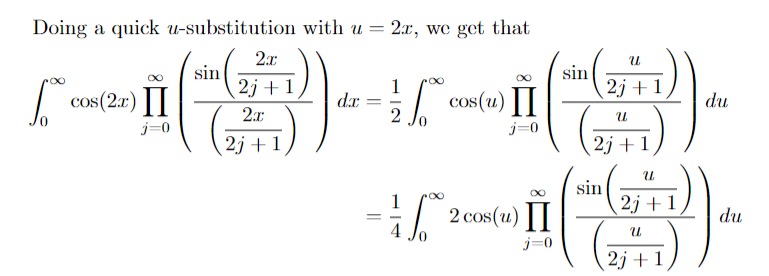Back

@robinhouston - an amusing fact: in 1995, in a paper on the arXiv, Kent Morrison said "we might conjecture" that

$${\int }_0^{\mathrm{\infty }}\prod _{n=1}^{\mathrm{\infty }}\cos (x/n)dx\stackrel{?}{=}\pi /4$$

$${\int }_0^{\mathrm{\infty }}\cos (2x)\prod _{n=1}^{\mathrm{\infty }}\cos (x/n)dx\stackrel{?}{=}\pi /8$$

Both these are false, of course! I read about this here:

https://mathoverflow.net/q/354932/2893

@seano @johncarlosbaez @robinhouston wow

@johncarlosbaez @robinhouston @JadeMasterMath Yeah so by "an infinite version of the cosine Borwein integral" I'm referring to the limit of the Borwein integrals (or at least the limit of their integrands, there may be some convergence issues at play).

In this case in particular, its the integral of 2cos(𝑥) times the product of sin(𝑥/𝑛)/(𝑥/𝑛) for all odd n. My claim relies on this limit actually equaling a value close to π/2, which I don't have a proof for yet, but it seems like it should work.

@johncarlosbaez @robinhouston @JadeMasterMath And this strategy should also apply to that case! The same essential product-swapping argument should allow you to conclude that integral is the "infinite version of the Borwein integral", the integral of just the product sin(𝑥/𝑛)/(𝑥/𝑛) for all odd n. So if the limit of this also equals something close to π/2, this explains that case as well.

@johncarlosbaez @robinhouston @JadeMasterMath Indeed, the fact that this second integral has a much larger difference from π/4 than the first integral from π/8 probably comes from the fact that the normal Borwein integral differs from π/2 much more quickly than the cosine Borwein integral. So presumably the limit of the normal integrals will be much farther from π/2 than the limit of the cosine integrals. And specifically these limits should allow us to calculate the observed differences we see!

@seano @robinhouston @JadeMasterMath - so by "cosine Borwein integral" I guess you mean something like

$${\displaystyle {\int }_0^{\mathrm{\infty }}2\cos x\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}\cdots \frac{\sin (x/(2n+1))}{(x/(2n+1))}dx}$$

This equals $\pi /2$ for $2n+1\le 111$ and then starts getting smaller:

https://en.wikipedia.org/wiki/Borwein_integral

This seems extremely related to what you've done, but again I don't know what happens as $n\to +\mathrm{\infty }$.

(2/n, n = 2)

@johncarlosbaez @robinhouston @JadeMasterMath Yep exactly! I played around with the limit of the normal Borwein integrals on wolframalpha and it appears to converge to a value close to pi/2, but I don’t know if any ways to prove this or the related conjecture for the limit of the cosine Borwein integrals.

But we could support this conjecture numerically by approximating these limits and comparing them to the integrals. I haven’t done this to much precision, but so far it does seem to work!

@seano @robinhouston @JadeMasterMath - neat! There's a formula for the normal Borwein integrals in the section "General formula" here:

https://en.wikipedia.org/wiki/Borwein_integral#General_formula

It's not really a closed form, but it might help us show

$$\underset{n\to +\mathrm{\infty }}{lim}{\displaystyle {\int }_0^{\mathrm{\infty }}\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}\cdots \frac{\sin (x/(2n+1))}{(x/(2n+1))}dx}$$

is just slightly less than π/2. And there may be a similar formula for the limit we actually care about now.

@gregeganSF - since you're a whiz on Mathematica, maybe you could numerically investigate

$${\displaystyle {\int }_0^{\mathrm{\infty }}2\cos x\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}\cdots \frac{\sin (x/(2n+1))}{(x/(2n+1))}dx}$$

for large $n$ and see if it's close to $\pi /2$. It's exactly $\pi /2$ for $2n+1\le 111$.
But if it stays very close to $\pi /2$ as $n\to +\mathrm{\infty }$ then @seano may have just solved our mystery!

@robinhouston @JadeMasterMath

@johncarlosbaez I’m not @gregeganSF, and I’m no whiz on Mathematica, but I can say that evaluating

NIntegrate[
2 Cos[x] Product[Sinc[x/i], {i, 1, 100001, 2}], {x, 0, Infinity},
WorkingPrecision -> 50]

gives a value that matches π/2 to 41 decimal places

@robinhouston @gregeganSF - wow! So, if @seano's calculations here are correct - and I haven't found a mistake yet - this "explains" the mystery below.

"Explains" in quotes because all it does is reduce this mystery to the question of why

$${\displaystyle \underset{n\to +\mathrm{\infty }}{lim}{\int }_0^{\mathrm{\infty }}2\cos x\frac{\sin x}{x}\prod _{i=0}^n\frac{\sin (x/(2i+1))}{x/(2i+1)}dx}$$

is so close to $\pi /2$. But this is a tractable question since we know why it's $\pi /2$ for $n\le 55$.

@johncarlosbaez @gregeganSF @seano I also wonder if @gjm’s mini-thread at https://mathstodon.xyz/@gjm/109627311459780458 might explain it a level more deeply, though i’m not sufficiently facile with Fourier transforms to have understood it properly yet.

@gregeganSF - yes, I think that studying those repeated convolutions can put a lower bound on the infinite limit and eventually explain what's going on here.

This may require more of a taste for analysis than any of us have. But I feel the puzzle has now switched from a mystery to something that just requires some careful work.

@robinhouston @seano

@johncarlosbaez @gregeganSF @robinhouston I decided to take a look at the original paper by the Borweins to see if they had any insights, and I found out that apparently this might not be an open problem after all? On page 15 and 16 of https://carma.edu.au/resources/db90/pdfs/db90-119.00.pdf, they derive the identity in essentially the same way I did, and then even show how to obtain lower bounds on the limit (although I don’t fully understand that part). So that’s a fun turn of events! :p

@seano - Nice! I was reading some similar things in other papers by them, but not quite this.

So yes, they knew the tricks you discovered. On page 16 of the pdf file you cite, they say that "lengthy numerical computation" shows that a quantity we're interested in is less than 10⁻⁴¹. Knowing this solves the mystery, in some sense. @robinhouston showed essentially the same thing by running a short Mathematica program.

But I still think a good analyst could find a more conceptual proof!

@robinhouston @johncarlosbaez @seano

That seems to make sense, but either there must be a flaw in the argument, or I’m calculating something incorrectly.

The rectangular pulses we convolve have half-widths a_i=1/(2i-1), which gives variances a_i^2/3, and the sum of these is π^2/24.

I get the value of the Gaussian with that variance, evaluated at x=1, being 0.184428, as compared to 0.25 for the iterations that give π/2 for the integral. So that’s waaay too low!

@johncarlosbaez @gregeganSF @seano @gjm Oh, I thought it satisfied Lyapunov's condition? I'll check that.

@robinhouston @johncarlosbaez @gregeganSF @seano I don't _think_ it does, but I make a lot of mistakes and am not an expert on this stuff, so I could very well be wrong.

@seano @johncarlosbaez @gregeganSF @gjm Very much same! (This is why I don't like analysis very much: too many technical side-conditions for my taste.) Let's check.

@robinhouston @seano @johncarlosbaez @gregeganSF @gjm Yeah I don’t think the CLT applies here, but the Kolmogorov three series theorem applies and shows that it is almost surely convergent to a well defined random variable, which is why the Fourier transform shouldn’t be expected to decay to zero.

@seano @R4_Unit @gjm @johncarlosbaez @gregeganSF Ah, thank you! That theorem is new to me. So (if I've understood) it converges provided that sum of the squares of the pulse-widths does, but not necessarily to a Gaussian.

@robinhouston @seano @gjm @johncarlosbaez @gregeganSF in this case yes. The first series relates to tail behavior (trivial for us), the second to means after discarding tails (all zero for us), the third to the variance (finite). This provides an if and only if condition for the almost sure convergence of a random series.

@robinhouston @seano @gjm @johncarlosbaez @gregeganSF you can also use a Berry-Essen estimate to bound the distance from a Gaussian (https://en.wikipedia.org/wiki/Berry%E2%80%93Esseen_theorem then scroll to “non-identical summands)

@johncarlosbaez that's about right, yes! I like the questions, but the answers sometimes make me feel confused and sad

@jamestwebber - yes, Greg Egan and I have already thought about the stuff in that video - and now Sean O has done some calculations that show exactly how that old stuff is connected to the current puzzle! So I think the mystery is dissipating.

Here's the sort of thing Greg knows how to prove:

@johncarlosbaez I guess I'm unclear on what the specific mystery is for this example. The question of "why does it do that" seems broadly answered, but maybe you have a more specific question you're trying to solve

@jamestwebber -

When I posted my question, I didn't know why the integral I wrote down is about

π/8 - 7.4×10⁻⁴³

That was the specific mystery. It was by no means "broadly answered" in my mind - it was very mysterious.

However, in response to my post, Sean O has done a calculation which makes this fact much easier to understand:

https://mathstodon.xyz/@seano/109627356107653590

So now the solution is in sight, and I can easily imagine mathematicians filling in the remaining details.

@johncarlosbaez

I don't know if you watched the whole thing, but I think the second half of 3blue1brown's video is really useful here for illustrating what's happening. And as Sean O posted, I think this is probably shown (in a general way) in the original paper: https://mathstodon.xyz/@seano/109628832603525145

@jamestwebber - happy new year! Yes, these "patterns that eventually fail" are quite shocking at first. Some people find them discouraging, but once I understood a bit about why they happen, I started liking them.

@AndresCaicedo - I don't go around saying that to everyone. But Robin and I have been talking about the failure of these identities for days now. There are papers about them, and whole web page about them:

https://mathworld.wolfram.com/InfiniteCosineProductIntegral.html